Электротехнический-портал.рф

В настоящее время экономически обоснованные уровни количественных характеристик безотказности работы электродвигателей отсутствуют.

В принципе безотказность работы, например АД, можно довести до самого высокого уровня за счет применения специальных мер, в том числе: улучшения конструкции электродвигателей, выбора установленной завышенной мощности, разработки комплекса спецзащит от аварийных режимов, осуществления непрерывного контроля за рациональными условиями эксплуатации электродвигателей и т.д.

Однако многие из этих мероприятий связаны со значительными финансовыми и другими затратами и экономически себя не оправдывают. Например, нет острой необходимости и целесообразности принимать меры к тому, чтобы срок службы подшипников в электродвигателе был в несколько раз больше срока службы самого электродвигателя, или недопустимо, например, повышать безотказность работы электродвигателя за счет снижения производительности технологического оборудования.

С другой стороны, специалисты, работающие в области повышения надежности электрических машин, справедливо подчеркивают, что затраты при эксплуатации электродвигателей с повышением уровня их безотказности значительно снижаются. С ростом технико-экономических показателей (коэффициента мощности и коэффициента полезного действия) уровень надежности электрических машин повышается.

Поэтому одной из важных задач оптимизации, в частности, асинхронных двигателей является изыскание оптимального уровня безотказности работы электродвигателей, удовлетворяющего минимальным затратам при максимальном экономическом эффекте.

Успешным решением задачи оптимизации безотказных режимов работы электродвигателей является полная ликвидация износовых отказов и максимально возможное предупреждение внезапных отказов.

Для этих условий с целью правильного изыскания экономического критерия оптимизации можно использовать экспоненциальный однопараметрический закон распределения вероятностей, являющийся частным случаем двухпараметрического закона Вейбулла-Гнеденко. Для этого закона постоянной величиной является интенсивность (опасность) отказов, 1/ч:

λ = const.

Стоимость (цену) Ц годового обслуживания (эксплуатации) электрической машины можно представить в виде двух слагаемых, одно из которых Ц₀ не зависит от количественных показателей безотказности работы электродвигателя, а другое Ц´(λ) является функцией параметра безотказности [24], т.д.

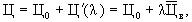(24)

где 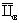- средняя цена восстановления отказавшего электродвигателя.

Если повысить безотказность работы электродвигателей, т.е. снизить интенсивность отказов с λ₁ до λ₂, то годовая экономия ∆Э затрат на эксплуатацию электродвигателей станет равной

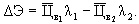(25)

Когда речь идет об увязке технико-экономических показателей с уровнем надежности работающего объекта, то под технико-экономическими показателями понимаются начальные (капитальные) затраты К и ежегодные эксплуатационные издержки И, приведенная сумма которых (к одной размерности) и составляет общие расчетные затраты З.

Возрастание капитальных затрат оправдывает себя в том случае, если оно приводит не только к обеспечению надлежащего уровня безотказности работы объекта, но и к снижению эксплуатационных издержек, в результате чего уменьшаются и общие расчетные затраты.

Экономию на эксплуатационные расходы ∆И можно совместить с экономией от ущерба при простоях оборудования, пользуясь следующим выражением:

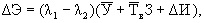(26)

где 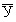- средний ущерб от отказов электродвигателей;

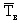- среднее время на восстановление отказавших электродвигателей;

З - годовые условные потери, З = const.

Второй сомножитель в формуле (26) представляет собой среднюю стоимость отказов.

Для определения связи параметра безотказной работы электродвигателей с дополнительными капитальными вложениями априори можно принять, что последние являются функцией отношения параметров, т.е.

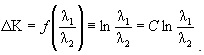(27)

Из уравнения (27) видно, что дополнительные капитальные затраты пропорциональны уровню безотказности работы электродвигателей, т.е. возрастают (снижаются) при его повышении (снижении), что и выражено приемлемой для данного случая логарифмической функцией

С = const,

где С - параметр, определяющий постоянную затрат на повышение безотказности работы электродвигателей.

Этот параметр численно равен приращению стоимости объекта при уменьшении интенсивности отказов в е раз (2,71 раз).

Окончательно дополнительный экономический эффект ∆U от повышения уровня безотказности работы электродвигателей, приведенный к одной размерности, руб., можно представить как

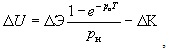(28)

где 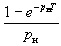- показатель времени, характеризующий какой-то приведенный момент времени Т_пр, произведение которого на значение эффекта и позволит получить приведенный эффект ∆U;

р_н - нормативный коэффициент эффективности дополнительных капитальных вложений, значение которого обратно нормативному времени окупаемости, т.е. 1/6,7 = 0,15.

С увеличением срока службы Т электродвигателей приведенный момент времени стремится к 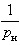, что дает основание утверждать об ограниченном значении приведенного эффекта.

С учетом формул (26) и (27) можно получить математическую зависимость дополнительного экономического эффекта:

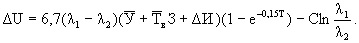(29)

По уравнению (29) можно определить оптимальный уровень безотказности работы электродвигателей, который и принимают за максимум дополнительного экономического эффекта:

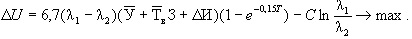
Для определения оптимальной интенсивности отказов уравнение (29) следует продифференцировать по λ₂ с последующим приравниванием производной нулю:

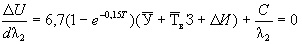(30)

Следовательно,

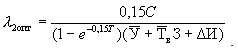(31)

Из этой формулы видно, что оптимальное значение интенсивности отказов λ_2опт электродвигателей не зависит от начального значения λ₁ и определяется только отношением постоянной затрат к средней стоимости отказа.

Если значение λ_2опт подставить в формулу (29), то после несложных преобразований можно определить максимальный экономический эффект, полученный за счет повышения уровня безотказности работы электродвигателей, и необходимые для этих целей капитальные вложения (см. вычитаемые в формулах (29) и 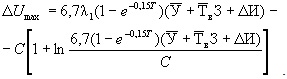(32)):

(32)

Если оптимальная интенсивность отказов λ_2опт не зависит от начального значения интенсивности отказов λ₁ электродвигателей, то максимальный экономический эффект уже существенно будет зависеть от λ₁, что видно из формул (29) и (30):

• при λ₁ = λ_2опт∆U_max = 0;
• при λ₁ > λ_2опт∆U_max > 0 и с увеличением разницы между λ₁ и λ_2опт значение ∆U_max возрастает;
• при λ₁ < λ_2опт∆U_max < 0, что означает отсутствие дополнительного эффекта и наличие ущерба из-за значительных затрат и низкой экономичности работы электродвигателей.

Из уравнения (30) также видно, что максимальный экономический эффект зависит от исходного уровня интенсивности отказов λ₁ и срока службы электродвигателей, и функционально может быть выражен следующей зависимостью:

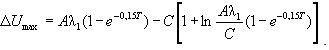(33)

где постоянная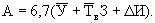

В общем виде зависимость дополнительного экономического эффекта ∆U от начального значения интенсивности отказов λ₁ и времени Т на основании формулы (29) можно выразить как

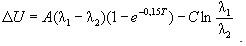(34)

Следовательно, формула (33) есть частный случай формулы (34) для одной лишь точки функции, соответствующей оптимальному уровню безотказности работы эксплуатируемых электродвигателей λ_2опт.

С учетом постоянной А получим, что

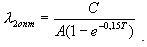(35)

Задавшись исходными значениями постоянных А, С и λ₂, построим график функции

∆U = f(λ₂,T).

В качестве примера возьмем данные отказов 300 асинхронных двигателей типа АОТ 63-4 номинальной мощностью 10 кВт для привода прядильных и крутильных машин.

Априори примем следующие средние значения постоянных:

A = 5·10⁷; С = 10; l₁ = 4·10^-5 при T = 0.

Годовое значение числа часов работы Т_г = 6000 ч для 3-сменных предприятий. В результате получим

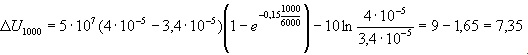
Следует отметить, что вычитаемое 1,65 представляет собой дополнительные капиталовложения. Определим

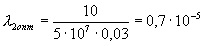
Используя формулу (34), в которой принимаем λ_2опт, или (33), получим значение максимального экономического эффекта:

по формуле (34)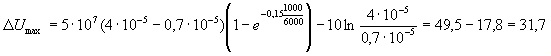 

по формуле (33)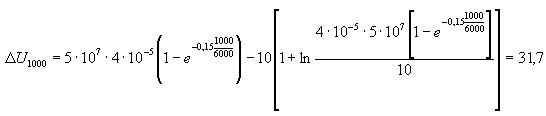 

В табл. 6 приведены расчетные данные для построения взаимосвязанных графиков функций λ₂, λ_2опт, ∆U, ∆U_max, ∆K_max и ∆К.

На рис. 7 показаны графики взаимосвязанных зависимостей всех величин, приведенных в табл. 6.

Из данных табл. 6 и графиков рис. 7 видно, что со снижением интенсивности отказов дополнительный экономический эффект монотонно возрастает и достигает максимума при λ_2опт.

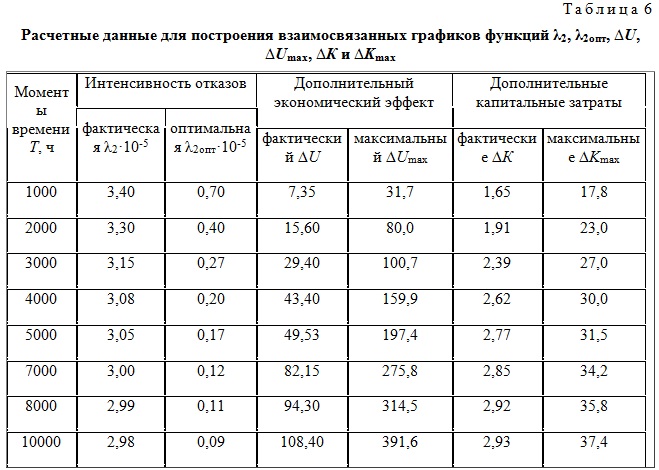
На графике рис. 7 можно выделить два многоугольника, один из которых abcdefg характеризует фактические (текущие) значения экономического эффекта, дополнительных капитальных затрат и интенсивности отказов, а второй АВСDЕFG - соответствующие им максимальные и оптимальные значения.

Данные расчетов, приведенные в табл. 6, несколько условны, но становятся достаточно точными, если известны конкретные значения постоянных средних затрат С на повышение безотказности работы электродвигателей и стоимости А отказов. При других значениях этих постоянных, отличающихся от принятых в данном расчете, дополнительный и максимальный экономический эффекты и капитальные затраты, а также оптимальные значения интенсивности отказов электродвигателей несколько изменятся, но общий характер указанных выше соотношений останется прежним.

Расчеты показали, что если затраты на разработку и внедрение спецзащит по повышению уровня безотказности работы электродвигателей составляют малую долю (не выше 1 - 5 %) общих затрат на технологическое оборудование и если при этом не наблюдаются значительные потери производительности и брака продукции, то в принципе нецелесообразно ограничивать повышение уровня безотказности работы этих электродвигателей из-за чисто экономических соображений.

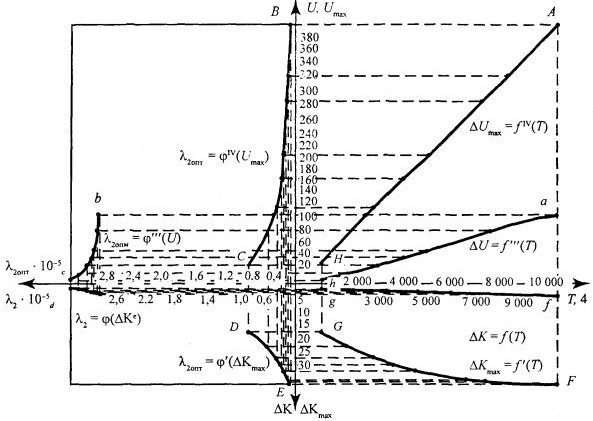
Рис. 7. Графики взаимосвязей интенсивностей отказов с экономическим эффектом и дополнительными капитальными затратами

Можно считать, что мероприятия по повышению уровня безотказности работы электродвигателей эффективны тогда, когда средние затраты на предупреждение одного отказа меньше среднего удельного ущерба, вызываемого одним отказом.

Наличие полученных математических моделей позволяет экономически обосновать оптимальный уровень безотказной работы приводных электродвигателей (в частности, АД) оборудования и дает возможность разработать необходимый комплекс организационно-технических мероприятий по предупреждению и устранению отказов.