Электротехнический-портал.рф

Простая трехфазная цепь – это симметричная, трехфазная цепь, с сосредоточенными активными и индуктивными сопротивлениями при отсутствии в ней трансформаторных связей.

Источник бесконечной мощности – источник, собственное сопротивление которого равно нулю и его напряжение, изменяясь с постоянной частотой, имеет неизменную амплитуду.

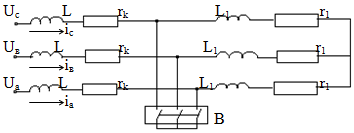
Рис.1. Простейшая цепь

U_a = U_mSin(ω + α),

где α – фаза включения фиксирует момент возникновения КЗ.

После включения выключателя B цепь распадается на два участка. В правой части цепи после КЗ, энергия, запасенная в индуктивности L₁, будет переходить в тепло, поглощаясь сопротивлением r₁, при этом в дифференциальном уравнении равновесие для каждой фазы участка можно записать так:

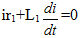
его можно решить относительно тока:

i=i₀e^-t/Ta1

где Т_а1 – постоянная затухания, она определяется исходя из сопротивления:

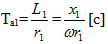
В левом участке схемы будет продолжаться переходный процесс за счет имеющегося питания со стороны источника, т.е. в этом участке будет существовать принужденный ток. Он будет сдвинут на некоторый угол относительно предшествовавшего тока.

Дифференциальное уравнение относительно фазы А:

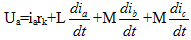
т.к. i_b+i_c=-i_a тогда можно записать

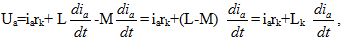
где L_k=L-M – результирующая индуктивность фазы с учетом влияния других фаз

В общем виде для любой фазы:

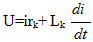
Решение этого уравнения будет:

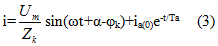
где Z_k – полное сопротивление цепи КЗ;

φ_{к –} угол сдвига тока в цепи КЗ относительно напряжения источника той же фазы.

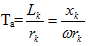
Т_а – постоянная времени цепи КЗ.

В уравнении (3) ток i – это сумма двух слагаемых:

1) принужденный ток или периодическая слагающая тока,

2) свободная составляющая или апериодическая составляющая тока.

i_kt=i_пt+i_at

Начальное значение тока (t = 0)

i_k(0) = i_п(0) + i_a(0), отсюда

i_a(0) = i_k(0) - i_n(0) =I_msin(α-φ)-I_nmsin(α-φ_k)

где I_msin(α-φ) – полный ток предшествующего режима;

I_nmsin(α-φ_k) - периодическая составляющая тока КЗ;

i _k(0) – начальное значение I_кз, которое с учетом невозможности изменения тока скачком в цепи с индуктивностью, равно i₍₀₎, т.е. току предшествующего режима в данной фазе к моменту t=0.

На векторной диаграмме (рис.2):

t - неподвижная ось времени;

U_a, U_b, U_c, I_a, I_b, I_c – характеризуют предшествующий режим;

φ – угол сдвига между U и I;

α – момент возникновения КЗ;

I_пa, I_пb, I_пc – характеризуют установившийся после КЗ режим в цепи;

φ_к – угол сдвига тока в цепи при КЗ.

i_a(0) является проекцией (I_m-I_пm) на ось времени.

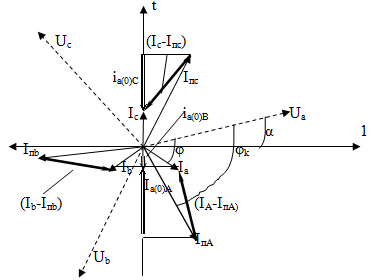
Рис.2. Векторная диаграмма

В зависимости от фазы включения КЗ начальное значение i_a(0) может меняться. Его значение будет максимальным, если в момент включения КЗ разность векторов (I_m – I_пm), будет параллельна оси t, т.е.:

1) при α = 0 и отсутствии предшествовавшего тока в цепи,

2) при х_к >>r_k имеем φ_к ≈ 90⁰, в этом случае будет возникать наибольший апериодический ток, и будет достигнут максимум мгновенного значения тока КЗ(Рис.3).

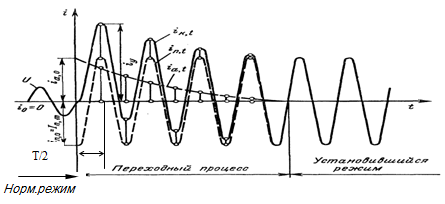
Рис.3. Изменение полного тока и его составляющих.

Максимальное мгновенное значение I_кз называется ударным током i_у. Считают, что он наступает примерно через полпериода (Т/2). При f = 50Гц, Т/2 = 0,01сек. с момента возникновения КЗ.

С учетом условий 1) и 2), т.е. φ_к ≈90⁰ и α = 0:

i_y = I_пm + I_пme^-0,01/Ta = k_yI_пm,

где k_y = 1 + e^-0,01/Ta – ударный коэффициент, показывает превышение ударного тока над амплитудой периодической слагающей I_кз.

1 < k_y < 2

k_y = 1 при Т_а = 0 (L_к = 0)

k_y = 2 при Т_а = ? (r_k =0)

Чем меньше Т_а, тем быстрее затухает i_a, следовательно, тем меньше k_y. Влияние i_a сказывается лишь в начальный момент переходного процесса, т.к. в сетях и установках ВН i_a затухает через 0,1–0,3с, а в установках НН она практически незаметна.

Действующее значение полного тока в произвольный момент времени (среднеквадратичное значение тока за один период, в центре которого находится рассматриваемый момент времени):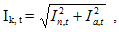

где 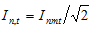 - действующее значение периодической слагающей тока за один период;

I_nmt - амплитуда огибающей периодической слагающей тока в момент времени t (в общем случае const);

I_a,t ≈ i_a,t- действующее значение апериодической составляющей за один период,

i_a,t- мгновенное значение  в момент, находящийся на середине этого периода.

Наибольшее действующее значение полного тока КЗ – I_y имеет место за первый период переходного процесса при условии, когда i_a(0) = I_nm: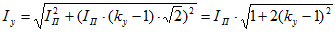  

Определение Т_а в сложной разветвленной цепи:

1) точное( Из ТОЭ): нахождение i_своб. в любой ветви достигается применением преобразований Лапласа, т.е. с использованием операторного метода. Такой общий и строгий путь решения даже для небольшой схемы требует большой вычислительной работы (достаточно вспомнить, что каждая параллельная ветвь с r и L увеличивает на один порядок степень характеристического уравнения). Поэтому для практических расчетов используют:

2) приближенное решение:

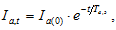
где 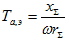- эквивалентная постоянная времени,

x_∑, r_∑ - суммарные реактивное и активное сопротивления схемы.

3) грубое определение Т_а. При более грубых расчетах не прибегают к подсчету Т_{а, э}, а определяют ее в соответствии с k_у. Например, при k_y ≥ 1,8 – Т_а = 0,045с, одно и то же для всех ветвей схемы.