Электротехнический-портал.рф

Проводниковые материалы в основном служат для передачи электрической энергии и ее непосредственного преобразования в тепловую, механическую и другие виды энергии. Проводниками могут служить твердые тела, жидкости и газы. Твердыми проводниками являются металлы, различного рода сплавы, модификации углерода и композиции на их основе. К жидким проводникам относятся расплавленные металлы и различные электролиты. Большинство металлов являются жидкими проводниками лишь при повышенных температурах.

Электролитами являются водные растворы кислот, солей, щелочей и расплавы ионных соединений.

Все газы и пары металлов становятся проводниками при высокой напряженности приложенного электрического поля. Основным условием при этом является возникновение ударной или фотоионизации и газ может стать проводником с электронной и ионной электропроводимостью. При равенстве количества положительных и отрицательных заряженных частиц в объеме сильно ионизированного газа получают равновесную проводящую среду так называемого четвертого состояния вещества – плазму.

К основным характеристикам проводниковых материалов относятся: удельное сопротивление и удельная проводимость; температурный коэффициент удельного электрического сопротивления; термоэлектродвижущая сила (термоэдс); теплопроводность; теплостойкость; предел прочности на разрыв и относительное удлинение при разрыве (рисунок 5.1).

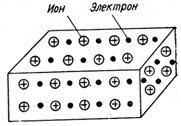
Рисунок 5.1 – Схема строения металлического проводника

Знание этих характеристик позволяет оценить электрические, тепловые и механические свойства проводникового материала.

Удельное сопротивление материала ρ является основ­ной величиной, характеризующей материал проводника. Для измерения удельного сопротивления проводников обычно поль­зуются образцами, изготовленными из исследуемого материала в виде отрезков проводов неизменного сечения. В этом случае, зная сопротивление R, площадь поперечного сечения S и длину L образца, удельное сопротивление материала можно вычис­лить, исходя из следующего известного соотношения

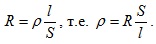(5.1)

В Международной системе единиц (СИ) ρ измеряют в ом­метрах (Ом×м). Однако на практике для оценки удельного со­противления проводников широко пользуются внесистемной единицей Ом·мм²/м, связанной с единицей СИ соотношением 1 Ом-мм²/м = 10^-6 Ом×м = 1 мкОм×м

Удельное сопротивление проводников находится в пределах от 0,016 для серебра до 1,6 мкОм-м для фехралей (жаропроч­ных сплавов на железохромовой основе), т. е. имеет диапазон в два порядка.

Часто применяется величина, обратная удельному сопротивлению и носящая название удель­ной проводимости, которая равна

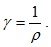(5.2)

Так как величина, обратная электрическому сопротивлению и называемая проводимостью, измеряется в единицах Си в сименсах (1/Ом = 1 См), то единица удельной проводимости равна 1 См/м.

Удельное сопротивление (а следовательно, и удельная проводимость) в основном зависят от средней длины свободного пробега электрона в данном проводнике, которая, в свою очередь, зависит от строения материала проводника. Все чистые металлы с наиболее правильной кристаллической решеткой характеризуются наименьшими значениями удельного сопротивления, а примеси, искажая решетку, приводят к увеличению его. Даже небольшое наличие примеси (приблизительно 0,5 %) приводит к увеличению ρ на 5÷55 %.

Значительное возрастание ρ наблюдается при сплавлении двух металлов в том случае, если они образуют твердый раствор, т. е. образуют при затвердевании совместную кристаллизацию и атомы одного металла входят в кристаллическую решетку другого.

Повышенная электропроводность проводниковых материалов обусловлена большим количеством обобществленных электронов, которые классической электронной теорией металлов рассматриваются как электронный газ .

В соответствии с этими представлениями свободные электроны находятся в состоянии хаотического теплового дви­жения со средней скоростью и, сталкиваясь с колеблющимися атомами кристал­лической решетки. Среднее расстояние l, проходимое электроном между двумя столкновениями, называют длиной свободного пробега, средний промежуток вре­мени между двумя столкновениями – временем свободного пробега. Время свобод­ного пробега вычисляется по формуле

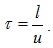(5.3)

Средняя кинетическая энергия электронов, находящихся в непрерывном хаоти­ческом движении, линейно зависит от температуры

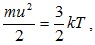(5.4)

где k =1.38·10^-23 Дж/К – постоянная Больцмана. Температуре T= 300 К соответ­ствует 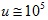м/с.

Распределение электронов по энергетическим состояниям, характеризуемое ве­роятностью р(Е), подчиняется статистике Максвелла – Больцмана и описывает­ся экспоненциальной функцией

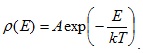(5.5)

При этом считается, что в каждом энергетическом состоянии может находиться любое число электронов, а при температуре абсолютного нуля энергия всех сво­бодных электронов равна нулю.

Если в проводнике существует электрическое поле, то под действием этого поля элек­троны приобретают ускорение, пропорциональное напряженности поля Е, в резуль­тате чего возникает направленное движение электронов со средней скоростью

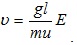(5.6)

Такое направленное движение называют дрейфом электронов, оно накладывает­ся на хаотическое движение электронов. Скорость дрейфа значительно меньше скорости теплового движения. Направленное движение электронов создает ток, плотность которого равна

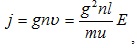(5.7)

где n – концентрация электронов.

Этот ток пропорционален напряженности поля, коэффициентом пропорциональ­ности является удельная электрическая проводимость

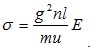(5.8)

Классическая теория, давая в целом правильное представление о механизме элект­ропроводности, не учитывает распределение электронов по энергетическим со­стояниям. Поэтому она не может объяснить ряд противоречий теории с опытны­ми данными, в частности, классическая теория не в состоянии объяснить низкую теплоемкость электронного газа. Более полное представление о процессах, происходящих внутри вещества, дает современная квантовая физика.

Электропроводность создается свободными электронами, способными покинуть атомы. Такой способностью обладают только валентные электроны. Поэтому в дальнейшем речь пойдет только об электронах, находящихся на энергетических уровнях валентной зоны.

Квантовая физика исходит из того, что электроны могут находиться на строго определенных энергетических уровнях, энергетическая плотность которых вблизи границ энергетических зон изменяется по параболическому закону (рисунок 5.2 а)

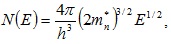(5.9)

где 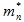– эффективная масса электрона, учитывающая взаимодействие электро­на с периодическим полем кристаллической решетки, то есть это масса свободно­го электрона, который под действием внешней силы смог бы приобрести такое же ускорение, как и электрон в кристалле под действием той же силы.

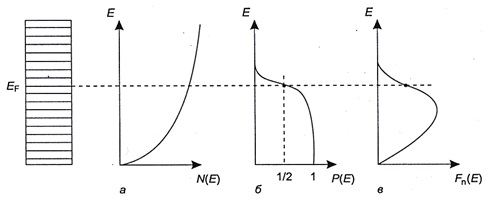
Рисунок  5.2 – Энергетическая плотность энергетических уровней электронов

В соответствии с принципом Паули на каждом энергетическом уровне могут нахо­диться два электрона с противоположными спинами. Если концентрация свобод­ных электронов равна n, то при температуре абсолютного нуля они займут n/2 самых низких энергетических уровней. Наиболее высокий из занятых уровней называется уровнем Ферми и обозначается Ет. При нагреве кристалла электронам сообщается тепловая энергия порядка kT, вследствие чего некоторые электроны, находящиеся вблизи уровня Ферми, переходят на более высокие энергетические уровни. Избыток энергии, получаемый электронами при нагреве проводника, очень незначителен по сравнению с энергией Ферми, при комнатной температу­ре он равен 0,026 эВ (1 эВ = 1,61019 Дж). Поэтому средняя энергия свободных электронов сохраняется практически неизменной, а незначительное изменение средней энергии означает малую теплоемкость электронного газа. В квантовой теории вероятность заполнения энергетических уровней электрона­ми определяется функцией Ферми–Дирака (рисунок 5.2,б)

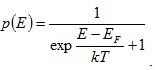(5.10)

Из формулы (5.10) следует, что уровень Ферми представляет собой энергетический уро­вень, вероятность заполнения которого равна 1/2.

Распределение электронов по энергиям (рисунок 5.2, в) определяется энергетической плотностью разрешенных уровней и вероятностью их заполнения

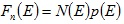(5.11)

Концентрация электронов может быть найдена путем интегрирования по всем заполненным состояниям

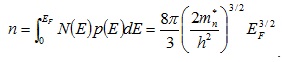(5.12)

Если считать, что атомы в металле ионизированы однократно, то концентрация свободных электронов будет равна концентрации атомов, которая рассчитывает­ся по формуле

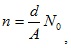(5.13)

где d – плотность материала; А – атомная масса; N₀ – число Авогадро (6,02 · 1023 моль-1).

Следовательно, уровень Ферми, отсчитанный от дна валентной зоны, может быть найден из уравнения (5.12)

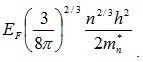(5.14)

Величина энергии Ферми для различных металлов лежит в пределах от 3 до 15 эВ. Если в проводнике создать электрическое поле с напряженностью Ет, то электро­ны, расположенные вблизи уровня Ферми, переходят на более высокие энергети­ческие уровни, приобретая добавочную скорость направленного движения

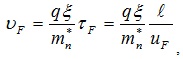(5.15)

где τ_F – время свободного пробега; u_F– тепловая скорость быстрых электронов, обладающих энергией, близкой к энергии EF.

Электроны, находящиеся на глубинных уровнях, вероятность заполнения кото­рых равна 1, непосредственно реагировать на внешнее поле не могут, так как все ближайшие энергетические уровни заняты. Однако несмотря на это они участву­ют в процессе электропроводности, перемещаясь на более высокие энергетиче­ские уровни по мере их освобождения. Поле начинает влиять на эти электроны тогда, когда они оказываются вблизи уровня Ферми. Таким образом, под действи­ем поля в движение приходит весь «коллектив» электронов. Скорость движения этого «коллектива» определяется скоростью движения электронов, находящихся вблизи уровня Ферми. С учетом этого обстоятельства выражение для плотности тока принимает вид

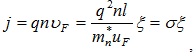(5.16)

где 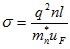– удельная электрическая проводимость. Учтем, что

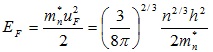(5.17)

Найдем отсюда 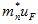и, подставив найденное значение в (5.16), получим

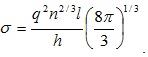(5.18)

Концентрация свободных электронов в чистых металлах различается незначи­тельно. Поэтому удельная электрическая проводимость металлов определяется средней длиной свободного пробега электронов, которая зависит от структуры атомов и типа кристаллической решетки.

В чистых металлах с идеальной кристаллической решеткой единственной причи­ной, ограничивающей длину свободного пробега электронов, являются тепловые колебания атомов в узлах кристаллической решетки, амплитуда которых возрас­тает с ростом температуры. Интенсивность столкновений электронов с атомами, то есть их рассеяние, прямо пропорциональна поперечному сечению сферическо­го объема, занимаемого колеблющимся атомом, и концентрации атомов. Следо­вательно, длина свободного пробега будет равна

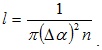(5.19)

Потенциальная энергия атома, отклонившегося на величину Δα от узла кристал­лической решетки, определяется соотношением

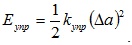(5.20)

Здесь k_упр – коэффициент упругой связи, которая стремится вернуть атом в по­ложение равновесия.

Поскольку средняя энергия колеблющегося атома равна kТ, то

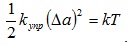(5.21)

Решая (5.21) относительно (Δα)² и подставляя полученный результат в (5.19), определяем среднюю длину свободного пробега электрона

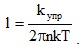(5.22)

Следовательно, удельная электрическая проводимость с ростом температуры уменьшается, а удельное электрическое сопротивление
ρ=1/σ возрастает. Влия­ние температуры на сопротивление проводника оценивают температурным коэф­фициентом удельного сопротивления

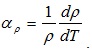(5.23)

У большинства металлов при комнатной температуре α_r ≈ 0,004 К-1. Если в металле имеются примеси, то помимо рассеяния на основных атомах возникает рассея­ние электронов на примесных атомах, в результате чего уменьшается длина сво­бодного пробега, определяемая соотношением

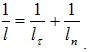(5.24)

Здесь 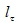и 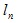характеризуют рассеяние на тепловых колебаниях основных атомов и примесей соответственно.

Этим объясняется то, что чистые металлы имеют более низкое удельное сопротивление по сравнению со сплавами.

На высоких частотах плотность тока изменяется по сечению проводника. Она максимальна на поверхности и убывает по мере проникновения в глубь проводника. Это явление называется поверхностным эффектом.

Неравномерное распределение тока объясняется действием магнитного поля тока, протекающего по проводнику. Магнитный поток, сцепленный с проводом, про­порционален току

Ф = Li,  (5.25)

где L – индуктивность проводника.

Если ток изменяется по синусоидальному закону i = Im sin ωt, то изменение магнитного потока вызывает появление ЭДС самоиндукции

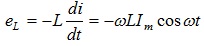(5.26)

Эта ЭДС имеет направление, противоположное току в проводе, и тормозит его изменение в соответствии с законом Ленца.

При прохождении переменного тока переменное магнитное поле возникает как вокруг проводника, так и внутри него. При этом потокосцепление максимально для внутренних слоев и минимально для внешних. Поэтому ЭДС самоин­дукции оказывается максимальной в центре проводника и уменьшается в направ­лении к поверхности. Соответственно, и плотность тока наиболее значительно ослабляется в центральной части проводника и в меньшей степени – у поверхно­сти, иначе говоря, происходит вытеснение тока к поверхности проводника. Оно тем сильнее, чем выше частота.

Распределение плотности тока по сечению проводника подчиняется экспоненци­альному закону

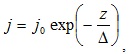(5.27)

где j₀ – плотность тока на поверхности; z – расстояние, измеряемое от поверхности; Δ – глубина проникновения тока.

Глубина проникновения тока, выраженная в миллиметрах, равна расстоянию, на котором плотность тока уменьшается в е = 2,72 раз по отношению к своему значе­нию на поверхности проводника. Она пропорциональна удельному сопротивлению ρ[Ом·м] и обратно пропорциональна частоте f [МГц]

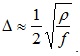(5.28)

В случае сильно выраженного поверхностного эффекта, когда ток протекает по тонкому поверхностному слою, толщина которого много меньше диаметра про­вода d, экспоненциальное распределение тока может быть заменено однородным распределением с постоянной плотностью тока в пределах тонкого слоя толщи­ной Д, на основании чего можно ввести понятие эквивалентной площади сечения проводника, занятой током

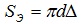(5.29)

Поскольку площадь сечения, через которое протекает ток, уменьшилась, то сопро­тивление провода переменному току R~ стало больше, чем его сопротивление по­стоянному току R₀, что учитывают коэффициентом увеличения сопротивления

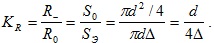(5.30)

Полученная формула справедлива при Δ << d.

Электрические свойства тонких пленок отличаются от свойств объемных провод­ников. Это объясняется изменением структуры проводящих пленок и, соответ­ственно, механизма перемещения электрических зарядов, создающих электрический ток. На рисунке 5.3 показаны три области, соответствующие трем различным механизмам протекания тока. При напылении пленки сначала образуются отдель­ные разрозненные островки (область 1), переход электронов происходит через узкие диэлектрические зазоры, что обусловлено термоэлектронной эмиссией и туннельным эффектом. В этой области удельное сопротивление очень велико, а температурный коэффициент отрицателен, так как с ростом температуры облегчается переход электронов от островка к островку.

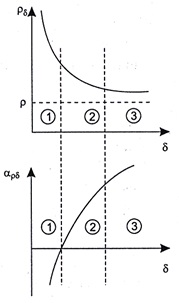
Рисунок 5.3 – Различные механизмы протекания тока в тонких плёнках

По мере напыления пленки происходит образование проводящих цепочек между отдельными остров­ками и начинает работать обычный механизм электропроводности, удель­ное сопротивление пленки уменьша­ется, а температурный коэффициент становится положительным (область 2). При дальнейшем напылении ос­тровки исчезают и образуется сплошная пленка толщиной около 0,1 мкм (область 3). На этом участке удельное сопротивление выше, чем удельное сопротив­ление монолитного проводника, что объясняется размерным эффектом, суть ко­торого состоит в сокращении длины свободного пробега электронов вследствие их отражения от поверхности пленки. Полагая, что процессы рассеяния элект­ронов в объеме и на поверхности независимы, можно для длины свободного про­бега 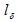электронов в пленке записать

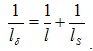(5.31)

Здесь l и ls – длины свободного пробега электронов при рассеянии в объеме и на поверхности.

Приближенно полагая длину свободного пробега при рассеянии на поверхно­сти l_S равной толщине пленки δ, получим

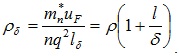(5.32)

Здесь ρ – удельное электрическое сопротивление монолитного проводника.

Сопротивление пленки определяется по формуле

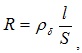(5.33)

где l – длина проводящей пленки; S – площадь поперечного сечения пленки.

Учитывая, что S = δω, где ω – ширина пленки, получаем

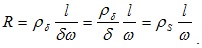(5.34)

Здесь 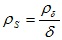– удельное поверхностное сопротивление. Величина ρS равна со­противлению пленки при условии 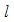= ω, то есть ρS представляет собой сопротив­ление пленки, имеющей форму квадрата.

Подбором толщины пленки можно изменять величину ρS независимо от удельно­го сопротивления материала.

В микроэлектронике в качестве соединительных пленок применяют пленки из чистого металла, чаще всего алюминия, а в качестве резистивных пленок – туго­плавкие металлы (вольфрам, тантал, рений, хром, молибден) и сплавы никеля с хромом.

Нагревостойкость твердых и жидких диэлектриков < Предыдущая		Следующая >Классификация магнитных материалов и требования к ним