Электротехнический-портал.рф

Исследования пробоя твердых диэлектриков по своему объему значительно превышают исследования всех других видов диэлектриков, что обусловлено более широким применением твердых диэлектриков. Это, в свою очередь, обусловлено  их высокими электрическими характеристиками в сочетании с удовлетворительными механическими и теплофизическими характеристиками. Механизм пробоя значительно отличается для разных диэлектриков и даже для одного и того же диэлектрика при разных условиях.

Закономерности пробоя твердых диэлектриков:

Температурная зависимость. Эта зависимость зачастую имеет достаточно сложный вид. Например в некоторых случаях электрическая прочность с ростом температуры сначала увеличивается затем уменьшается, в других случаях монотонно возрастает или убывает. Последний случай обычно хорошо описывается моделью теплового пробоя.

Пробивное напряжение, обусловленное нагревом диэлектрика, связано с частотой поля, условиями охлаждения диэлектрика, температурой окружающей среды; оно зависит также от нагревостойкости материала. С повышением температуры электрическая прочность уменьшается.

Для однородных плоских диэлектриков, обладающих потерями, существует приближенный метод расчета пробивного напряжения.

Для расчета U_пр полагаем, что пробой происходит при повышенных температурах и в диэлектрике преобладают потери от сквозной электропроводности. Таким образом, учитывая экспоненциальную зависимость тангенса потерь (tg δ) от температуры и используя выражение Ра = U ω С-tgδ, после преобразований получим

Pа = U2 f ε S tgδ eα(t – t0) / (1,8 1010 h), (3.1)

где U - приложенное напряжение; f - частота; ε. - диэлектрическая проницаемость материала; S - площадь электрода; tg δ - тангенс угла потерь диэлектрика при t 0 - температуре окружающей среды; α- температурный коэффициент тангенса угла потерь; t - температура нагретого за счет диэлектрических потерь материала; t 0 - температура электродов, приблизительно равная температуре окружающей среды; h - толщина диэлектрика.

Теплопроводность материала электродов обычно на два - три порядка больше, чем теплопроводность диэлектрика, поэтому полагаем, что теплота из нагревающегося объема диэлектрика передается в окружающую среду через электроды. Мощность, отводимая от диэлектрика, выражается формулой  Ньютона

Ра = 2 σ S (t - t0 ). (3.2)

где σ - коэффициент теплопередачи системы диэлектрик - металл электродов.

Для наглядности дальнейших рассуждений воспользуемся графическим построением, показанным на рисунок 3.1, где в выбранной системе координат изображены экспоненты тепловыделения  при различных значениях приложенного напряжения и прямая теплопередачи.

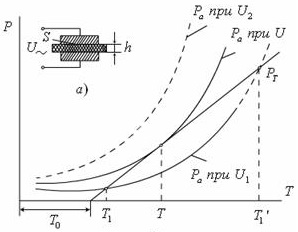
Рисунок  3.1 - Пробивное напряжение при тепловом факторе

На рисунке 3.1 изображены: прямая теплопередачи Рт = φ(t); экспоненты тепловыделения  для трех различных значений приложенного напряжения. При значении напряжения U₁, прямая теплопередачи является секущей кривой тепловыделения, и, следовательно, диэлектрик нагреется до температуры T₁температуры состояния устойчивого равновесия. Напряжение U₁ будет неопасным для образца, если нагрев до этой температуры не приведет к механическому и ш химическому разрушению структуры материала образца. Поэтому увеличим напряжение до значения U₁, при котором кривая тепловыделения станет касательной к прямой теплопередачи, что приведет к состоянию неустойчивого теплового равновесия при температуре T. При значении напряжения U₂ кривая тепловыделения пройдет выше прямой теплопередачи, а это означает отсутствие теплового равновесия, т.е. температура будет возрастать до разрушения диэлектрика - до теплового пробоя.

Таким образом, напряжение U, при котором имеет место неустойчивый режим - граничный режим, можно принять за напряжение пробоя U_пр.

Его значение можно определить по двум условиям

Ра = Рt,  (3.3)

dPa / dt = dP t / dt,  (3.4)

Решая эти два уравнения относительно Ui с учетом выше обозначенных значений для Ра и Рt, получаем

U2 f ε tgδ S eα(t – t0) / (1,8 1010 h) = 2 σ S (t – t0),  (3.5)

U2 f ε tgδ S eα(t – t0) / (1,8 1010 h) = 2 σ S,  (3.6)

Разделив эти два выражения, получим 1 / α = t – t 0, тогда, подставив его в последнее выражение и решив его относительно U, получим

U2пр = 1,8 1010 2 σ h / (f ε tgδ α),  (3.7)

или

Uпр = К ( σ h / (f ε tgδ α)1/2, (3.8)

где К – числовой коэффициент, равный 1,15 10 5, если все величины выражены в единицах системы СИ.

Отсюда следует, что пробивное напряжение будет выше ( изменяется по закону экспоненты), если диэлектрик будет толще, условия теплоотвода лучше (σ больше), частота ниже, а ε и tgδ меньше. При больших ε, tgδ и при высоких частотах, а также при большом температурном коэффициенте тангенса угла потерь пробивное напряжение будет ниже.

Этот расчет, пригодный только для одномерного потока теплоты, называется графоаналитическим и является приближенным, В нем не учтены перепад температуры по толщине диэлектрика (искажение электрического поля и повышение градиента напряжения в поверхностных слоях), а также теплопроводность материала электродов. Поэтому тепловой пробой часто наступает при напряжении ниже расчетного. Более точные методы расчета разработаны академиками Н.Н. Семеновым и ВА. Фоком только для изделий простейшей конфигурации.