ррРазность между результатом измерения ХИ и истинным значением измеряемой величины х, как известно, называется абсолютной погрешностью результата измерения:
Δ=хи-х
Погрешность является случайной величиной. Она может быть представлена в виде уравнения:
Δ=Δc+Δ0,
где Δc – математическое ожидание величины, а Δ0 - случайная величина с нулевым математическим ожидаем.
Неслучайную величину Δc называют систематической погрешностью, а Δ0 – случайной погрешностью.
Если значение Δc известно, то систематическую погрешность можно исключить, приняв за окончательный результат исправленный результат измерения:
Хиспр=Хи - Δc
Случайную погрешность Δ исключить нельзя, так как неизвестно, какое конкретное значение приняла случайная величина Δ при данном измерении. Для оценки влияния случайной погрешности на результат измерения принимают положительные Δ1 и Δ2 и находят вероятность того, что измеряемая величина х заключена между (хи- Δ2) и (хи+ Δ1). Интервал [хи- Δ2;хи+ Δ1] называется доверительным интервалом, а вероятность того, что x находится внутри этого интервала - доверительной вероятностью Pд. Можно показать, что Pд=Р[-Δ1≤Δ≤Δ2].
Как правило, при решении всех вероятностных задач выбирают Δ1=Δ2, тогда Pд=P(|Δ|<Δ1). Если известен дифференциальный закон распределения погрешности Δ; т.е. плотность вероятности f (Δ), то

Вероятный смысл дифференциальной функции распределения (по определению) есть
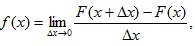
Нам известно, что F(x+Δx)-F(x) – означает вероятность того, что случайная величина х примет значение, принадлежащее интервалу (х, х + Δх). Таким образом, предел отношения вероятности того, что непрерывная случайная величина примет значение, принадлежащее интервалу (х, х + Δх), к длине этого интервала (Δx→0), будет равен значению дифференциальной функции в точке х. (По аналогии с определением плотности заряда в точке целесообразно рассматривать значение функции f(х) в точке х как плотность вероятности в этой точке). Числовые характеристики закона распределения ƒ(Δ) – математическое ожидание Δ(m), дисперсия d(D) и среднее квадратичное отклонение σ могут быть определены по формулам
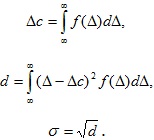
Математическое ожидание погрешности измерения есть случайная величина, относительно которой рассеиваются другие значения погрешностей при повторных измерениях. Математическое ожидание характеризует систематическую составляющую погрешности измерения относительно истинного значения измеряемой величины. В частном случае, при нормальном законе распределения погрешностей.

В этом случае, пользуясь таблицей Лапласа Ф(z), можно определить доверительную вероятность:
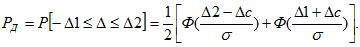
При использовании свойств функции Лапласа Ф(z) необходимо учитывать, что Ф(z) = -Ф(z).
В ряде случаев закон распределения погрешностей известен, однако известны (обычно приближенно) и его числовые характеристики Δc и σ. Тогда для грубой оценки снизу доверительной вероятности Рд при заданном симметричном доверительном интервале Δ1 можно воспользоваться неравенством Чебышева:
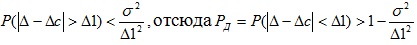
Значения результата измерения, подчиняющегося нормальному закону с очень высокой вероятностью, должны группироваться в пределах этого доверительного интервала.
В метрологии для выявления принадлежности отдельного результата измерения пользуются специальными критериями грубых погрешностей, наиболее простой из них – правило трех сигм: "Если при многократном измерении одного и того же постоянного размере сомнительное значение результата измерения отличается от среднего значения больше, чем на 3σ, то его следует отбросить, ибо вероятность того, что подобное отклонение является обычным следствием рассеяния экспериментальных данных, ничтожно мала".
Дисперсия погрешности характеризует степень разброса (рассеивания) отдельных значений погрешности относительно математического ожидания. Чем меньше дисперсия, тем меньше разброс, тем точнее вычисления.
Следовательно, дисперсия служит характеристикой точности проведенных измерений. Однако дисперсия выражается в единицах погрешности, возведенной в квадрат. Поэтому в качестве числовой характеристики измерений используют среднее квадратичное отклонение 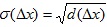 с положительным знаком, выражаемое в единицах погрешности:
с положительным знаком, выражаемое в единицах погрешности:
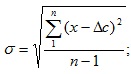
здесь 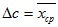 ; n – число измерений.
; n – число измерений.
Если случайная величина У связана с независимыми случайными величинами У1,У2,… Уn неизвестной функциональной зависимостью У = F (У1, У2, …), то зная математические ожидания mу1, mу2, mу2, … mуn и средние квадратические отклонения
σу1, σу2 …σуn, величин У1, У2, … Уn можно приближенно найти математическое ожидание mу и среднее квадратическое отклонение σу величины У по формулам

где 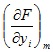 - частная производная функции F (У1 , У2 , …Уn ) по УI, взятая в точке (mу1, mу2, …mуn).
- частная производная функции F (У1 , У2 , …Уn ) по УI, взятая в точке (mу1, mу2, …mуn).
Пусть У1, У2, …Уn – случайные результаты прямых независимых измерений различных физических величин, а У = F (у1, у2, …уn) – результат косвенного измерения.
Тогда среднее квадратическое отклонение случайной погрешности результата прямого измерения есть Уi, а частная производная берется в точке у1, у2, …уn, соответствующей результатам прямых измерений. Систематическая погрешность Δc результата косвенного измерения связана с систематическими погрешностями Δс1, Δс2, …Δсn соответствующих прямых измерений, и определяется равенством

Если закон распределения погрешностей ƒ(Δ), а также его числовые характеристики Δc и σ неизвестны, то можно найти их приближенно, располагая результатами ряда неизвестных измерений (наблюдений) одной и той же величины. Приближенные значения Δc и σ величин – называют оценками.
В случае если произведено n независимых наблюдений одного и того же известного значения х (например с целью проверки прибора) и получены результаты х1, х2, …хn, то получим оценки
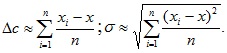
При неизвестной величине х (произведено n независимых наблюдений одного и того же неизвестного значения) найти оценку систематической погрешности Δc невозможно. Если в этом случае можно пренебрегать систематической погрешностью, то в качестве оценки истинного значения измеряемой величины следует принять среднее арифметическое наблюдений:
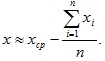
Уравнение среднего квадратического отклонения величины имеет вид
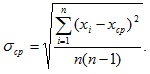
Среднее квадратическое отклонение каждого отдельного наблюдения, характеризующее точность метода измерения, определяют по уравнению

Предполагая, что закон распределения среднего арифметического результатов наблюдений близок к нормальному (имеет место при достаточно большем числе наблюдений), и пренебрегая систематической погрешностью, можно определить

Если известно, что погрешности отдельных наблюдений распределены по нормальному закону (параметры которого неизвестны), то вместо приближенной формулы следует использовать точное выражение:
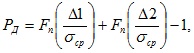
где Fn(t) – интегральная функция распределения Стьюдента.
Это выражение справедливо для любых n, больших единицы. Когда число наблюдений n мало (n < 10+20), а закон распределения погрешностей отдельных наблюдений нельзя считать близким к нормальному, то применение приближенного выражения приводит к значительным погрешностям.
В этом случае для грубой оценки величины имеет смысл использовать неравенство Чебышева, считая что σ=σср.
Пусть производится эксперимент по исследованию зависимости физической величины у от физической величины х. Известно, что у и х связаны зависимостью вида
у =φ(х, с1, с2, … сk),
где φ – известная функция, а с1, с2, … сk - неизвестные параметры. Например, у =ах+b, где а и b – неизвестные.
Требуется найти вероятные значения параметров с1, с2, …сk, если произведено n независимых опытов и получено n экспериментальных точек (хi, уi), причем n больше k.
Если координаты х1, х2, …хn известны с пренебрежимо малыми погрешностями, а погрешности измерений ординат у1, у2, … уn распределены по нормальному закону с нулевым математическим ожиданием и одним и тем же средним квадратическим отклонением, то наиболее вероятные значения с1, с2, …сk можно найти по методу наименьших квадратов из системы уравнений:
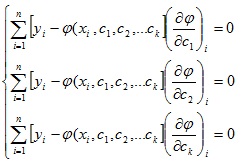
где 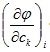 - значения частной производной функции φ по параметру сk в точке хi.
- значения частной производной функции φ по параметру сk в точке хi.
Поскольку при исследовании измерительной информации чаще всего проходится оценивать неизвестные параметры распределения случайных величин, то встает вопрос о характере, точности этих оценок.
Для того, чтобы статические оценки давали "хорошие" приближения оцениваемых параметров, они должны удовлетворять определенным требованиям: несмещенности оценки; эффективности; состоятельности 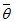 .
.
Несмещенной называют статистическую оценку 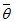 , математическое ожидание которой равно оцениваемому параметру θ при любом объеме выборки (т.е. при любом количестве измерений): М (
, математическое ожидание которой равно оцениваемому параметру θ при любом объеме выборки (т.е. при любом количестве измерений): М (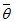 )= θ .
)= θ .
Смещенной называют оценку, математическое ожидание которой не равно оцениваемому параметру.
Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию.
При рассмотрении выборок большого объема (n – велико) к статистическим оценкам предъявляется требование состоятельности.
Состоятельной называют статистическую оценку, которая при n→∞ стремится по вероятности к оцениваемому параметру.
Например, если дисперсия несмещенной оценки при n→∞ стремится к нулю, то такая оценка оказывается и состоятельной. Таким образом, при неограниченном увеличении количества измерений n, если математическое ожидание равно оцениваемому параметру и отклонение наблюдаемых значений от оцениваемого параметра будет стремиться к нулю, то оценка будет состоятельной.
Условия несмещенности оценки является обязательным. Действительно, представим, что оценка 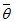 дает приближенное значение θ с избытком, когда каждое найденное по данным измерений число
дает приближенное значение θ с избытком, когда каждое найденное по данным измерений число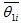 (i=1,…, k) больше истинного значения θ. В этом случае и математическое ожидание (среднее значение) случайной величины
(i=1,…, k) больше истинного значения θ. В этом случае и математическое ожидание (среднее значение) случайной величины 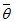 будет больше чем θ, т.е. М (
будет больше чем θ, т.е. М (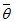 )>θ . Очевидно, что если дает оценку с недостатком, то М(
)>θ . Очевидно, что если дает оценку с недостатком, то М(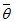 )<θ.
)<θ.
Таким образом, использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, привело бы к систематическим ошибкам ,т.е. неслучайным ошибкам, искажающим результаты измерения в одну определенную сторону). Например, измерение длины растянутой рулеткой систематически дает заниженные результаты. Поэтому естественно потребовать, чтобы математическое ожидание оценки 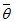 было равно оцениваемому параметру.
было равно оцениваемому параметру.
Хотя соблюдение этого требования не устранит ошибок (одни значения 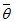 больше, а другие меньше
больше, а другие меньше 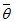 ), однако ошибки разных знаков будут встречаться одинаково часто. Иными словами, соблюдение требования несмещенности оценки гарантирует от получения систематических ошибок. Однако было бы ошибочным считать, что несмещенная оценка всегда дает достаточное приближение оцениваемого параметра. Действительно, возможные значения
), однако ошибки разных знаков будут встречаться одинаково часто. Иными словами, соблюдение требования несмещенности оценки гарантирует от получения систематических ошибок. Однако было бы ошибочным считать, что несмещенная оценка всегда дает достаточное приближение оцениваемого параметра. Действительно, возможные значения 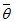 могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия D(
могут быть сильно рассеяны вокруг своего среднего значения, т.е. дисперсия D(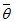 ) окажется значительной. В этом случае найденная по данным выборки оценка, например
) окажется значительной. В этом случае найденная по данным выборки оценка, например 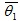 , может оказаться весьма удаленной от среднего значения
, может оказаться весьма удаленной от среднего значения 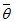 , а значит, и от самого оцениваемого параметра θ; приняв
, а значит, и от самого оцениваемого параметра θ; приняв 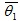 в качестве приближенного значения θ, мы допустили бы большую ошибку. Если потребовать, чтобы дисперсия была малой, то возможность допустить большую ошибку будет исключена. По этой причине к статистической оценке предъявляется требование эффективности.
в качестве приближенного значения θ, мы допустили бы большую ошибку. Если потребовать, чтобы дисперсия была малой, то возможность допустить большую ошибку будет исключена. По этой причине к статистической оценке предъявляется требование эффективности.
Точечной называют оценку, которая определяется одним числом. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам.
По этой причине при небольшом объеме выборки следует пользоваться так называемыми интервальными оценками. Интервальной называют оценку, которая определяется двумя числами, определяющими концы интервала.
Интервальные оценки позволяют установить точность и надежность оценок (определение этих понятий изложено выше). Заметим, что важнейшей особенностью характера ошибок измерения может служить вывод о законе их распределения.
Теорема. Если случайная величина представляет собой сумму очень большого числа независимых случайных величин  , влияние каждой величины на всю сумму ничтожно мало, то величина
, влияние каждой величины на всю сумму ничтожно мало, то величина 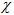 имеет распределение вероятностей, близкое к нормальному.
имеет распределение вероятностей, близкое к нормальному.
Например. Пусть производится измерение некоторой физической величины при помощи измерительного прибора. Любое измерение, как известно, характеризует лишь приближенное число измеряемой величины, так как на результат измерения оказывают влияние очень многие случайные факторы. В силу того, что число этих факторов (измерение температуры, колебания показаний прибора и др.) велико, совокупное их действие дает уже заметную суммарную ошибку.
Рассматривая суммарную ошибку как сумму большого числа взаимных независимых ошибок, можно сделать вывод, что эта суммарная ошибка будет иметь распределение вероятности, близкое к нормальному.
Далее рассмотрим примеры на выяснение оценок параметров, если при этом уже известен закон распределения вероятностей (нормальное, равномерное, и т.д.), (см. прил.1, табл.1).
Примечание. Приведем зависимость между систематической постоянной погрешностью θ, математическим ожиданием результатов наблюдений М1, случайной погрешностью Δc, результатом единичного измерения х и истинным значением измеряемой величины Q. Поскольку систематическая постоянная погрешность θ - это есть отклонение математического ожидания М результатов измерений от истинного значения измеряемой величины, то справедливо соотношение
θ = М – Q.
Случайной погрешностью Δc обычно называют разность между результатом единичного наблюдения х и математическим ожиданием результатов измерений М, т.е. Δc= х – М. Таким образом, получим
Q=x-θ -Δc.
Пример 3.1. Погрешность измерения напряжения ΔU распределена по нормальному закону, причем систематическая погрешность ΔUc=0, а σ=50 мВ. Найти вероятность того, что результат измерения отличается от истинного значения напряжения U не более, чем на 120 мВ.
Решение. При условии Δc=0 и Δ1=Δ2 следует, что
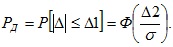
Воспользовавшись этой формулой и подставив значение функции Лапласа, получим
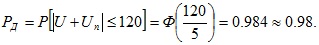
Ответ. ≈0,98.
Пример 3.2. Решить пример 3.1 при условии, что систематическая погрешность ΔUс равна 30 мВ.
Решение. Если в результате измерения Un не вносить поправку, учитывающую систематическую погрешность, то для нахождения искомой доверительной вероятности можно воспользоваться соотношением
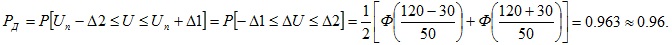
Ответ. ≈0,96.
Примечание. Если в результате измерения Un внести поправку, т.е. считать что Uиспр=Un- ΔUс, то получим

Сравнивая результаты, полученные в примерах 3.1. и 3.2., заметим, что для нормального закона распределения погрешностей при одинаковом доверительном интервале доверительная вероятность будет больше в том случае, когда ΔUc=0, или при внесении поправки в результат измерения (заметим, что поправка эта есть абсолютная погрешность, взятая с обратным знаком).
Пример 3.3. Погрешности результатов измерений, приведенных с помощью амперметра, распределены по нормальному закону σ=20мА. Систематической погрешностью можно пренебречь. Сколько независимых измерений нужно сделать, чтобы для одного из них погрешность не превосходила ±5 мА с вероятностью не менее 0,95?
Решение. Определим вероятность того, что при одном измерении погрешностьне превзойдет ±5 мА:
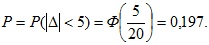
Найдем вероятность того, что при n независимых измерениях ни одного из них не обеспечит погрешности, меньшей 5 мА:
(1 – Р)n = 0,803n,
где (1-Р)n =1- 1,97=0,803 для одного единичного испытания.
Но, с другой стороны, эта же вероятность может быть определена из условия 1–0,95 = 0,05 Значит 0,803n≤0,05. Прологарифмируем неравенство и получим
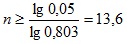
Поскольку число измерений n может быть только целым, то из условия n≥13,6 следует, что ближайшее целое есть 14; т.е. n≥14.
Ответ. n≥14.
Примечание. Если требуется оценить математическое ожидание с заданной точностью δ и надежностью  , то минимальный объем независимых измерений, обеспечивающей эту точность, может быть определен по формуле n=t2σ2/δ2, где t определяется из соотношения 2Ф(t)=
, то минимальный объем независимых измерений, обеспечивающей эту точность, может быть определен по формуле n=t2σ2/δ2, где t определяется из соотношения 2Ф(t)= по таблице функций Лапласа, σ – среднее квадратичное отклонение. При этом за n принимается наиболее близкое целое значение n.
по таблице функций Лапласа, σ – среднее квадратичное отклонение. При этом за n принимается наиболее близкое целое значение n.
Пример 3.4. Найти минимальное количество измерений, полученных с помощью амперметра с надежностью  =0,975. Точность независимых измерений не превышала бы 0,3А, если известно, что σ=1,2 (погрешность результатов измерений подчиняется нормальному закону).
=0,975. Точность независимых измерений не превышала бы 0,3А, если известно, что σ=1,2 (погрешность результатов измерений подчиняется нормальному закону).
Решение. Воспользуемся формулой, определяющей точность оценки математического ожидания:
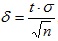 , отсюда n=t2σ2/δ2
, отсюда n=t2σ2/δ2
По условию  =0,975, следовательно, Ф(t)=0,975/2=0,4875, по таблице значений функции Лапласа найдем t = 2,24.
=0,975, следовательно, Ф(t)=0,975/2=0,4875, по таблице значений функции Лапласа найдем t = 2,24.
По условию δ=0,3, σ=1,2, тогда
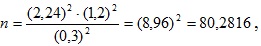
т.к. n – целое число, то наименьшее n=81.
Ответ. 81.
Пример 3.5. Погрешность результата измерения распределена равномерно от –1 до +3мА.
Найти: а) систематическую погрешность результата измерения; б) среднее квадратическое отклонение результата отклонения;
в) вероятность того, что исправленный результат измерения отличается от истинного значения измеряемого тока не более чем на 1 мА.
Решение. а) для равномерного распределения случайной величины имеем
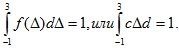 Отсюда
Отсюда 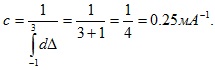
(Заметим, что распределение вероятностей называют равномерным на интервале, если на нем дифференциальная функция имеет постоянное значение. Для равномерного закона распределения характерны свойства  )
)
Таким образом, плотность распределения вероятности
С =f(Δ)=0,25мА-1.
По известным формулам получим требуемые характеристики
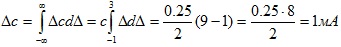 ,
,
б) далее определим
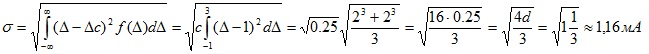
в) доверительную вероятность найдем по формуле
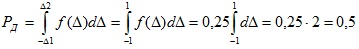
в нашем случае, по условию Δ1=Δ2=1мА.
Ответ. а) Δc=1мА; б) σ= 1,16 мА; в) Рд = 0,5.
Пример 3.6. Сопротивление r составлено из параллельно включенных сопротивлений r1 и r2, математические ожидания и средние квадратические отклонения которых известны: m1=12 Ом; m2=15 Ом; σ1 =1 Ом; σ2 =0,5 Ом.
Найти: а) математическое ожидание mr и среднюю квадратическую погрешность σT сопротивления r;
б) оценить вероятность того, что сопротивление r отличается от своего математического ожидания не более, чем на 1 Ом.
Решение: а) при параллельном соединении
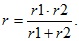
Тогда получим
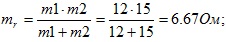
б) Найдем предварительно частные производные
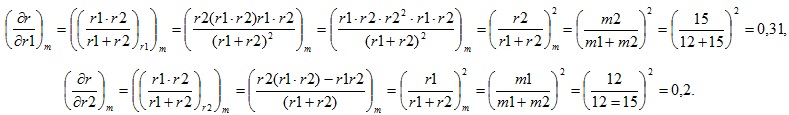
Согласно известной формуле получим искомую среднюю квадратичную погрешность сопротивления r:
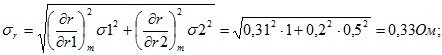
в) так как закон распределения погрешностей неизвестен, то воспользуемся неравенством Чебышева:

где Δ1=σ1 (по условию)
Ответ. а) m=6,67 Ом; σT= 0,33 Ом; б) Рд = 0,89.
Пример 3.7. Приведен ряд независимых наблюдений напряжения:
№ наблюдения … 1 2 3 4 5
U, мВ…………… 3790 3805 3832 3781 3842
Предполагая, что систематической погрешностью можно пренебречь, определить оценку истинного значения измеряемого напряжения U и средние квадратические погрешности метода измерения σ и результата измерения.
Решение. Воспользовавшись формулой

получим
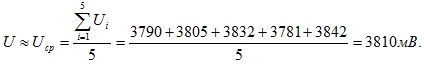
Для вычисления средней квадратической погрешности метода измерения используем формулу
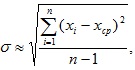
в наших обозначениях получим

Заметим, что, с одной стороны, среднее квадратическое отклонение величин хср определяют по формуле
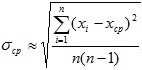 ,
,
с другой стороны, среднееквадратическое отклонение каждого отдельного наблюдения, характеризует точность метода измерения, при этом
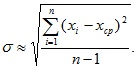
Очевидно, что  тогда получим искомое среднее квадратическое отклонение результата измерения:
тогда получим искомое среднее квадратическое отклонение результата измерения:
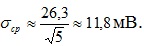
Ответ. σ=26,3 мВ; σср=11,8 мВ.
В условиях нашего примера найдем также доверительную вероятность того, что истинное значение измеряемого напряжения U отличается от Uср не более, чем на 30 мВ, и симметричный доверительный интервал ΔU2, соответствующий доверительной вероятности 0,95.
Решение. Заметим, что доверительная вероятность может быть вычислена по формуле
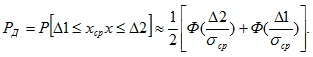
В нашем случае Δ1=Δ2=30 мВ, тогда искомая доверительная вероятность может быть вычислена по формуле (σср была определена нами раньше).

Искомый доверительный интервал определим из формулы для определения доверительной вероятности:
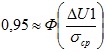 , следовательно,
, следовательно, 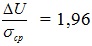
и тогда ΔU =1,96 · 11,8= 23 мВ.
Ответ. Рд =0,99; ΔU =23 мВ.
Рассмотренные примеры позволяют записать результаты обработки наблюдений в следующем виде: U=3810 ± 30 мВ с вероятностью Рд≈ 0,99; или U= 3810 ± 23 мВ с вероятностью Рд =0,95.
Если известно, что погрешности отдельных наблюдений распределены по нормальному закону (параметры которого неизвестны), то вместо приближенной формулы
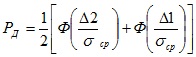
следует использовать точное выражение
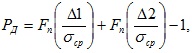
где F(t) – интегральная функция распределения Стьюдента.
Эта формула справедлива для любых n, больших единицы.
Примечание. Если число наблюдений n мало (n<10:20), а закон распределения погрешностей отдельных наблюдений нельзя считать близким к нормальному, то в этом случае для грубой оценки величины Рд имеет смысл использовать уже известное нам выражение (неравенства Чебышева)
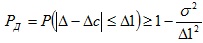 , положив в нем σ=σср
, положив в нем σ=σср
В условиях рассматриваемого выше примера, предположим, что погрешности наблюдений распределены по нормальному закону с нулевым математическим ожиданием.
Поставим задачи:
а) найти доверительную вероятность того, что истинное значение измеряемого напряжения U отличается от Uср не более, чем на 30 мВ;
б) найти симметричный доверительный интервал ΔU, соответствующий доверительной вероятности 0,95.
Решение: а) априорно известно, что закон распределения погрешностей является нормальным, поэтому следует для расчетов использовать точную формулу (с интегральной функцией распределения Стьюдента). Ранее нами были найдены Uср=11,8 мВ;
Δ1=Δ2=30мВ. Формула в этом случае примет вид
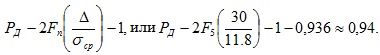
б) определим симметричный доверительный интервал:

По таблице значений интегральной функции распределения Стьюдента получим 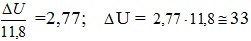 мВ.
мВ.
Таким образом, результат обработки данных может быть записан в виде
U=(3810±33) мВ с вероятностью Рд =0,95.
Ответ: а) Рд =0,94; б) ΔU=33 мВ.
Проведем анализ выводов, полученных при решении поставленных хадач.
Использование формулы 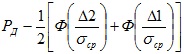 применительно к нормальному закону распределения погрешностей приводит к завышению точности результата измерения по сравнению с действительной точностью (при заданной доверительной вероятности получается меньший доверительный интервал, и наоборот, при заданном доверительном интервале получается большая доверительная вероятность).
применительно к нормальному закону распределения погрешностей приводит к завышению точности результата измерения по сравнению с действительной точностью (при заданной доверительной вероятности получается меньший доверительный интервал, и наоборот, при заданном доверительном интервале получается большая доверительная вероятность).
Пример 3.8. Получены результаты измерений удельного электрического сопротивления в зависимости от абсолютной температуры:
Т, К ……………..1178 1286 1489 1830 1988 2133 2289
g, 10-6 О 28,34 32,09 37,72 47,92 52,70 57,32 61,97
Исходя из предположения линейной зависимости вида p= с1Т+с2, определить коэффициенты с1 и с2.
Решение. Коэффициенты с1 и с2 найдем методом наименьших квадратов.
Заметим, что 
Тогда система уравнений примет вид
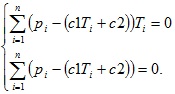
Раскроем скобки и преобразуем систему:

При n=7 получим уравнения для с1 и с2:

Произведя расчеты, получим:
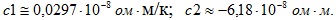
Тогда Т`i = ТI – Тср. Переменная такого вида называется центрированной.
Получим 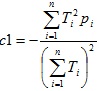 , а с2 можно определить и после подсчета с1.
, а с2 можно определить и после подсчета с1.
Получим Тср для данного примера 3.8:
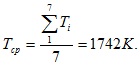
В результате вычислений получим:
|
Т` |
Тр` |
(Т`)2 |
|
-564 |
-16322 |
318096 |
|
-456 |
-14633 |
207936 |
|
-253 |
-9543 |
64009 |
|
88 |
4217 |
7744 |
|
246 |
12964 |
60516 |
|
390 |
22355 |
1521100 |
|
547 |
33898 |
299209 |
и определим коэффициенты: с1=0,029683; с2=6,1792.
Окончательно получим искомые коэффициенты
с1=0,0297 · 10-8 ом м/к, с 2 –6,18 · 10-8 Ом м.
| 1.1. Погрешности в метрологии< Предыдущая | Следующая >2. Электромеханические измерительные приборы |
|---|






